Nekompletnost dat a jejich imputace

V minulém cvičení šlo převážně o úpravu organizace dat v datové matici. Toto cvičení se zaměří přímo na vlastní obsah dat. Různé metody zpracování dat, které již znáte nebo s nimi budete teprve seznámeni, umožňují data znázorňovat a analyzovat jak s využitím vizuálních metod, tak rovněž těch numerických. Důležitým faktorem při zpracování dat je jejich původ – kdo data vytvořil, za jakým účelem. je důležité zjistit, zda data dávají smysl, zda jsou validní. Po úpravě organizace datové matice se přistupuje k průzkumové analýze dat, jejíž metody znáte z jiných cvičení. Nedílnou součástí práce s daty je však také explorace chyb či úplnosti datové matice.

Chybějící data jsou častou součástí téměř všech výzkumů, ale také datových matic získaných z jiných zdrojů, např. z vlastního měření. Anglicky jsou označována jako Missing Values. Více informací o této problematice naleznete např. na stránce MissingData. Tyto aspekty způsobují problémy a to hlavně z důvodu, že celá řada statistických programů předpokládají, že se pracuje s úplnou datovou maticí. Dalšími problémy je ovlivnění např. průměru, percentilů, regresních parametrů apod. Existuje celá řada přístupů, jak pracovat s těmito missings. Vždy je třeba zjistit, zda jsou tyto missing values náhodné nebo zde existuje nějaká podobnost = způsob náhrady by měl odpovídat způsobu vzniku těchto chybějících hodnot, nicméně ten je znám jen ojediněle a dá se zjišťovat s využitím např. statistických testů a vizualizačních nástrojů (např. hodnoty chybí jen u malých obcí; chybí u obcí v okrese Pardubice apod.). Pokud jsou chybějící hodnoty rozmístěny náhodně a nezávidí na hodnotách v jiných ukazatelích, tak se hovoří o Missing Completely At Random – MCAR (např. zapomněli jsme změřit hodnotu v jednom měřícím stanovišti, nezapsali jsme omylem hodnotu určitého ukazatele). Druhým případem mohou být situace nazývána Missing At Random – MAR. Ta může být vysvětlena na příkladu, kdy měření provádí studenti prvního a pátého ročníku a s vysokou pravděpodobností budou chybějící měření v případě studentů z prvního ročníku nebo pokud provádím měření v hustém lese, je větší předpoklad, že bude dané zaměření chybět (např. překročíme PDOP apod.). Chyba tak nezávisí na naměřené hodnotě, ale na tom, kdo nebo kde se měření provádí. Poslední variantou je Not Missing At Random – NMAR a existuje tedy vztah mezi měřenou hodnotou a výskytem missing values. Příkladem může být dotazování na výši platu, čím větší má dotyčný příjem, tím větší bude výskyt missing values (respondent odmítne vypovídat).

Pokud se tyto nedostatky ignorují analytikem, jsou velmi často ignorovány také softwarem, který je používán. Tento přístup bývá označován anglickými termíny complete case analysis nebo listwise deletion a je považován obecně za nevhodný. Příkladem může být jedna chybějící hodnota v tabulce níže v případě sloupce ZS (počet obyvatel ze základním vzděláním) v případě obce Bukovany. V případě complete case analysis by byl celý řádek Bukovany vyloučen ze zpracování. Dochází tak ke znepřesnění dat (přicházíme i o záznamy v ostatních ukazatelích).

Dalším přístupem k práci s chybějícími záznamy jsou metody tzv. imputace, kdy se snažíme tyto prázdné hodnoty nahradit. Jednou z těchto metod je např. simple mean imputation. Při použití této metody, je do prázdné buňky doplněna hodnota aritmetického průměru všech zbylých hodnot pro daný ukazatel. V našem případě by počet obyvatel se základním vzděláním byl roven 504 (ve skutečnosti je však 108!!). Z tohoto jednoduchého příkladu jsou patrné nedostatky této metody. Dalším příkladem imputace je využití regresní analýzy (regression mean imputation), kdy se hledá vztah mezi vybranými proměnnými a snažíme se vysvětlit závislou proměnnou (v našem případě obyvatelé se ZŠ vzděláním). Více se této problematice věnuji níže. Posledním způsobem je zpracování neúplných dat speciálními metodami.

Vizualizační nástroje pro chybějící hodnoty (Visualization of missing values)

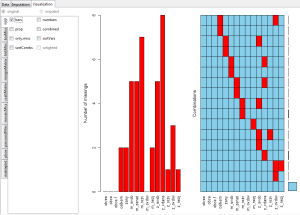
Aggregation Plot je nástroj používaný pro zjištění rozsahu výskytu missing values v datové matici. Levá část ukazuje podíl výskytu chybějících hodnot v jednotlivých ukazatelích, pravá část pak zobrazuje jednotlivé existující kombinace a jejich četnost ve sloupcovém grafu vpravo.

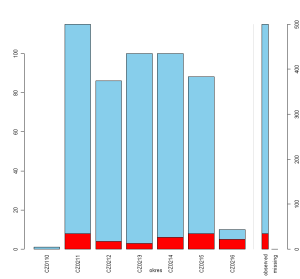
Histogram patří mezi běžně používané nástroje explorační analýzy dat. Své uplatnění nalézá také v případě vizualizačních technik při práci s chybějícími hodnotami. V tomto případě jsou chybějící hodnoty zobrazeny v samostatném sloupci, který je od zbylých hodnot oddělen mezerou. Alternativou je spine-plot, kdy četnostem odpovídá šířka daného sloupce.

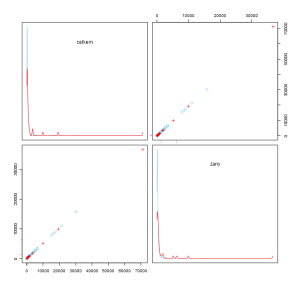
Velmi oblíbeným nástrojem je krabicový graf, resp. paralelní krabicové grafy, které zobrazují rozdělení hodnot jednotlivých proměnných a je možné odhalit vztah, kdy jedna spojitá proměnná vysvětluje rozložení chybějících hodnot v ostatních proměnných. Další možností je využití bodového grafu, který se často používá pro zobrazení vztahu mezi dvěma proměnnými. V případě, že jedna z těchto proměnných obsahuje chybějící hodnoty, tak je možné určit právě vztah mezi chybějícími hodnotami a hodnotami druhé sledované proměnné. V případě použití nástroje VIM jsou dále vykresleny také elipsy spolehlivosti, které umožňují snadnější identifikaci odlehlých pozorování (leží mimo danou elipsu). Dvourozměrný jitter plot slouží pro zobrazení kombinací chybějících hodnot dvou proměnných a to v grafu, který je rozdělen až do čtyř čtverců v případě, že obě analyzované proměnné obsahují chybějící hodnoty. Dále se využívají také maticové grafy, kde jsou chybějící hodnoty zobrazovány výraznou barvou, zatímco hodnoty známé jsou vykreslovány v odstínech šedi. V případě práce s kategoriálními daty je možné využít mozaikový graf, který zobrazuje vztah dvou a více proměnných s využitím plochy čtyřúhelníku, které jsou dále děleny podle počtu studovaných proměnných.

Metody imputace chybějících dat (Imputation of missing values)

Jak již bylo uvedeno v úvodu, tyto metody umožňují nahradit chybějící hodnoty náhradními hodnotami a to na základě použité techniky. Teprve po získání kompletní datové matice můžeme aplikovat standardní statistické metody (pokud chybějící hodnoty neignorujeme). Metod imputace je celá řada a dělí se na metody prosté (single) a mnohonásobné (multiple) imputace. V rámci tohoto cvičení se budeme zabývat jen první skupinou metod prosté imputace, kdy jsou chybějící hodnoty nahrazeny jednou novou hodnotou. V případě mnohonásobné imputace je chybějící hodnota nahrazena více hodnotami na základě předpokládaného rozložení.

Jednorozměrné metody prosté imputace

Chybějící hodnoty jsou nahrazeny pouze v rámci jedné proměnné. Do této skupiny je zařazena deduktivní imputace, kdy jsou chybějící hodnoty vyplněny na základě logického vztahu s jinými proměnnými a tak chybějící hodnota může být jednoduše dopočtena (suma do celkové hodnoty, kterou známe apod.). Další metodou v této skupině je nahrazení průměrnou hodnotou (viz úvod). Problémem této metody je fakt, že všechny chybějící hodnoty v rámci ukazatele budou mít stejnou hodnotu, dále víme, že průměr je velice citlivý na odlehlé hodnoty. Navíc pokud doplníme průměrné hodnoty, tak se nezmění průměr za celou proměnnou a tak nezískáváme novou informaci, ale jen doplňujeme kompletnost matice. Metoda se používá, pokud jsou chybějící hodnoty typu MCAR a i přes značné nevýhody bývá tato metoda pro svou jednoduchost často používána. Možným rozšířením by mohlo být využití prostorového sousedství okolo chybějící hodnoty (např. počet obyvatel s ZŠ vzděláním obce Bukovany by odpovídal průměru za okolní obce). Případně je možné použít jiný typ ukazatele polohy (medián, modus apod.).

Vícerozměrné metody prosté imputace

Náhrada chybějících proměnných probíhá ve více proměnných najednou a využívá se celá řada metod. Opět výše zmíněna regresní imputace vychází z klasické lineární regresní analýzy. Na základě záznamů proměnných s kompletně vyplněnými hodnotami (nezávislé proměnné) se vytvoří vztah pro ukazatel, který obsahuje chybějící hodnoty jež chceme nahradit a tvoří tak tedy závislou proměnnou. V případě vícerozměrné regresní imputace je to postup komplikovanější a musí se přistoupit k iteračnímu postupu. V prvním kroku jsou všechny chybějící hodnoty nahrazeny některou z metod jednorozměrných metod prosté imputace (např. nahrazení průměrem). V druhém kroku budeme imputovat nahrazené hodnoty v prvním sloupci s využitím hodnot v ostatních sloupcích. V dalších krocích budeme imputovat nahrazené hodnoty v dalších sloupcích, přičemž již budeme využívat nově nahrazené hodnoty regresní imputací v předešlých sloupcích.

Dalšími metodami pro náhradu chybějících hodnot jsou metody hot-deck imputace. Tato jednoduchá metoda má několik různých variant a obecně všechny z nich nahrazují chybějící hodnotu na základě hodnoty od jiného záznamu (tzv. dárce), který je podobný záznamu s chybějící hodnotou. Jednou za variant je náhodná hot-deck imputace (random hot-deck imputation – RHD), kdy je za dárce zvolen náhodně jeden ze skupiny vhodných dárců. Metoda se doporučuje pro použití v případě malého počtu chybějících hodnot v matici. Další metodou je sekvenční hot-deck imputace (Sequentional Hot-Deck imputation – SHD). Při hledání vhodného dárce se postupuje postupně od prvního řádku a hledá se nejvhodnější dárce. Data jsou seřazena podle důležitosti ostatních kritérií. Metoda je vhodná především pro prostorová data, které je možné seřadit podle souřadnic nebo podle příslušnosti do administrativního celku a hledat dárce v prostorové blízkosti záznamu s chybějící hodnotou. Také tato metoda se doporučuje pro soubory s malým počtem chybějících hodnot. Poslední představenou variantou je hot-deck imputace nejbližším sousedem (Nearest Neighbour Imputation), kdy je identifikován jediný dárce, který je nejvíce podobný danému záznamu s chybějící hodnotou. Tato podobnost je definována nejmenší vzdáleností, kdy se nejčastěji pracuje s Eukleidovskou vzdáleností. Nepracuje se však většinou v metrickém prostoru, ale v prostoru definovaným ostatními ukazateli.

K nahrazení chybějících hodnot se používá také metoda k-nejbližších sousedů, která bude vysvětlena v dalších cvičeních a obecně spočívá v tom, že je nalezeno k nejpodobnějších záznamů, přičemž k definuje uživatel. Výsledná hodnota pro nahrazení té chybějící se vypočtu jako aritmetický průměr nebo medián z hodnot v dané podobné skupině.

Posledním z představených metod je algoritmus IRMI (Iterative Robust Model-based Imputation), který narozdíl od ostatních dokáže pracovat i s rozdělením, které se ani neblíží normálnímu. Jedná se tedy o robustní metodu, která není ovlivněna odlehlými pozorováními apod. V každém kroku algoritmu je jedna proměnná použita jako vysvětlovaná, zatímco ostatní proměnní slouží k vysvětlení dané proměnné. Více informací o tomto algoritmu naleznete např. Templ, Kowarik, Filzmoser (2011) nebo Nárožná (2013).

Zadání

Projděte si postup imputace dat v IBM SPSS Statistics dle videí:

• video testující, zda jsou chybějící záznamy náhodné nebo je v nich nějaká pravidelnost (např. pravidelná vynechaná měření):

• vlastní imputace chybějících záznamů:

Samostatná práce:

1. Vyberte z dat dle vašeho výběru jednu intervalovou proměnnou (alespoň 70 záznamů)
2. Vymažte náhodně 10 % záznamů z této proměnné (Random selection)
3. Použijte vybrané metody imputace dat (metoda EM, mean value, median value, series mean)
4. Porovnejte výsledky imputace s originálními hodnotami dle průměrné odchylky
5. Interpretujte výsledky – uveďte s jakými daty pracujete a porovnání chyby

Data:

Data s chybějícími hodnotami
riginální data bez chybějících hodnot

Cvičení je vytvořeno v rámci projektu Inovace bakalářských a magisterských studijních oborů na Hornicko-geologické fakultě VŠB-TUO pod číslem CZ.1.07/2.2.00/28.0308. Tento projekt je realizován za spoluúčasti EU.